
More general questions of this kind on an arbitrary differentiable manifold are the subject of de Rham cohomology, which allows one to obtain purely topological information using differential methods.įurther information: Winding number Vector field corresponding to (the Hodge dual of) dθ.Ī simple example of a form that is closed but not exact is the 1-form d θ, i.e., that there are no magnetic monopoles. Reviews arent verified, but Google checks for and removes fake content.

On a contractible domain, every closed form is exact by the Poincaré lemma. Kershaw, 1971 - Differential calculus - 160 pages.
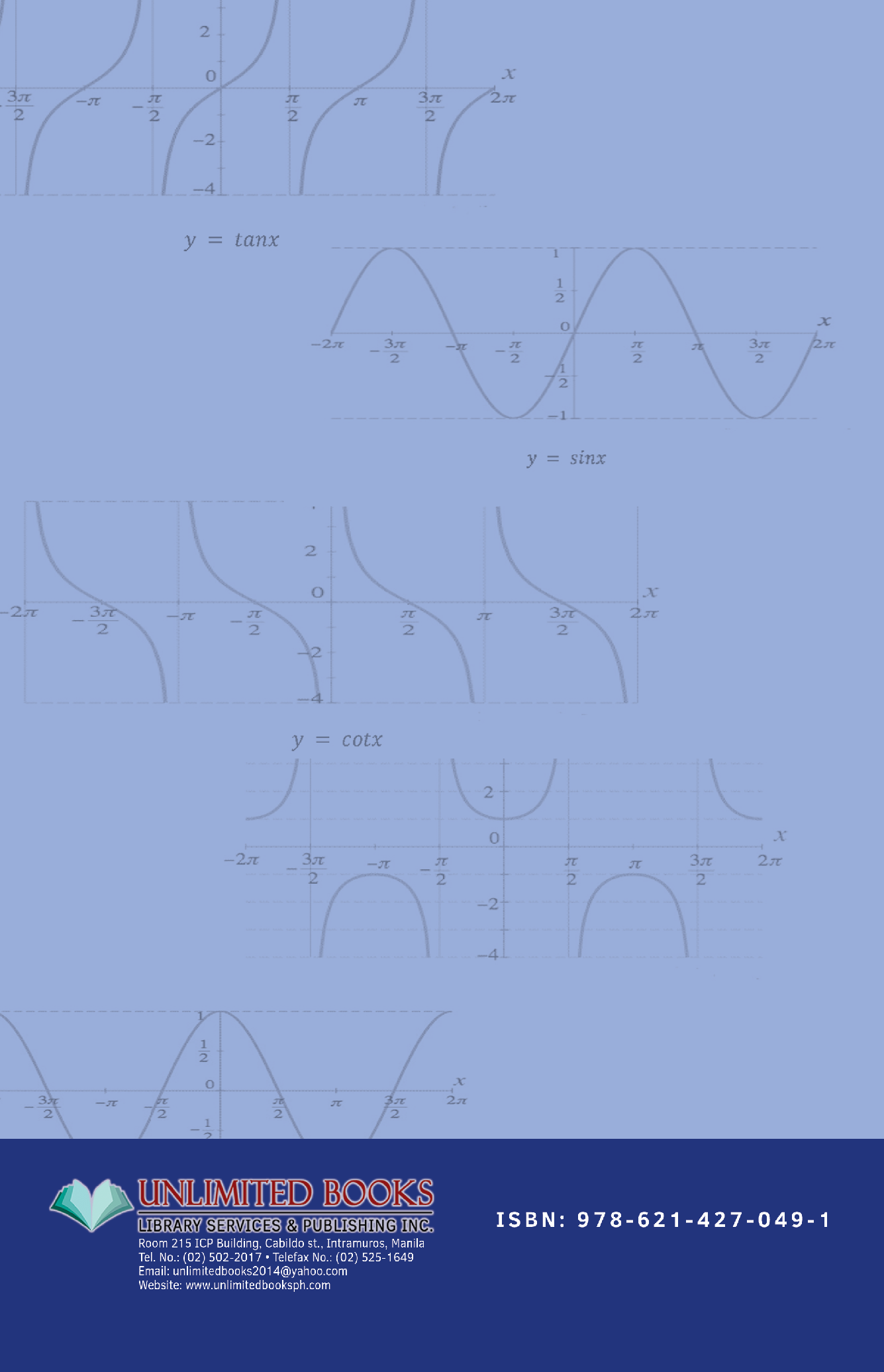
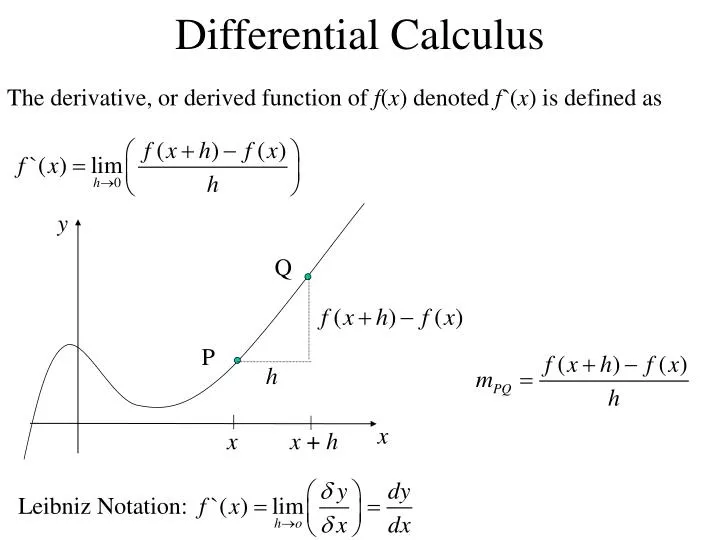
The question of whether every closed form is exact depends on the topology of the domain of interest. Since the exterior derivative of a closed form is zero, β is not unique, but can be modified by the addition of any closed form of degree one less than that of α.īecause d 2 = 0, every exact form is necessarily closed. The form β is called a "potential form" or "primitive" for α. Gouvêa ever taught was a vector calculus course for engineering students at the Universidade de São Paulo. 1.2Geometry-based Exterior Calculus The geometric nature of these models is best expressed and elu-cidated through the use of the Exterior Calculus of Differential Forms, rst introduced by Cartan Cartan 1945. Cartans work provides a superb text for an undergraduate course in advanced calculus, but at the same time it furnishes the reader with an excellent foundation for global and nonlinear algebra.Mathematical Review Brilliantly successful.
#Cartan differential calculus pdf
Thus, an exact form is in the image of d, and a closed form is in the kernel of d.įor an exact form α, α = dβ for some differential form β of degree one less than that of α. Henri cartan differential calculus pdf pdf download Indeed, it can easily be used for an honors course on differential equations that gives a completely rigorous treatment at the advanced undergraduate level. Many exercises with solutions make this book appropriate for learning the subject.In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero ( dα = 0), and an exact form is a differential form, α, that is the exterior derivative of another differential form β.
The book ends with an open program on symplectic diffeology, a rich field of application of the theory. we can consider x y 1: AnAn calculus as usual tells us what it means for this transition map to be smooth. We work on smooth manifolds: a smooth manifold is a space X together with an atlas of. and will pick up where differential topology left off. Janets algorithms on systems of linear partial differential equations. With its right balance between rigor and simplicity, diffeology can be a good framework for many problems that appear in various areas of physics.Īctually, the book lays the foundations of the main fields of differential geometry used in theoretical physics: differentiability, Cartan differential calculus, homology and cohomology, diffeological groups, fiber bundles, and connections. 10.The Maurer-Cartan form: 11.Characterizing the Maurer-Cartan form. Calculus of Variations and Partial Differential Equations. The category of diffeology objects is stable under standard set-theoretic operations, such as quotients, products, coproducts, subsets, limits, and colimits.

With a minimal set of axioms, diffeology allows us to deal simply but rigorously with objects which do not fall within the usual field of differential geometry: quotients of manifolds (even non-Hausdorff), spaces of functions, groups of diffeomorphisms, etc. Diffeology is an extension of differential geometry.


 0 kommentar(er)
0 kommentar(er)
